Each problem is on a separate sheet of paper.  Write your answer neatly in the space provided.  If you need more space (you shouldn't), there are a couple of extra sheets at the end of the exam, but please make sure that you indicate clearly the problem to which the comments apply.  Do NOT use any other paper to hand in your answers.

The exam is open book and notes.  Please do not ask or provide anything to anyone else in the class during the exam.  Make sure to ask clarification questions early so that both you and the others may benefit as much as possible from the answers.

Good luck.

Name:
 

ID#:

 

1. Boolean Algebra (10 points)

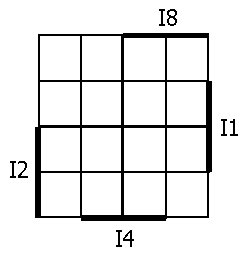
You are working with binary-coded decimal numbers and need to derive expressions that will indicate when an invalid number is present, that is, any 4-bit value greater than 9.  The function is F = ( {I8, I4, I2, I1} > 4'b1001).  Note that I8 is the high-order bit.  Fill in the Karnaugh map below for F.

(a) Derive a minimal sum-of-products expression.
 

I8 I4 + I8 I2

(b) List the essential prime implicants for this expression.
 

The two terms, I8 I4 and I8 I2, are both essential prime implicants.

(c) Derive a minimal product-of-sums expression.
 

(I8) (I4 + I2)

(d) Applying the rules of Boolean algebra transform the minimal P-o-S expression into the minimal S-o-P expression thereby proving that they are equivalent.
 

Applying the distributive law to the answer for part (c) yields the answer to part (a).

(e) Draw a circuit diagram for the mimized S-o-P function using only AND, OR, and NOT gates.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

2. Arithmetic (25 points)

Construct an adder that adds two 2-digit binary-coded decimal (BCD) numbers.  You have 4-bit adder modules available (with carry-in and carry-out) and any basic gates you require.  Hint: when adding two BCD digits that yield a result greater than 9, you can correct the value by adding an extra 6, of course, this may also cause a carry (e.g., 5 + 6 = 10 which, with another 6, yields 17 or a result of 1 with a carry of 1).
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

3. Combinational Logic (20 points)

Construct a circuit that determines whether a year is a leap year or not.  This is to be used in conjunction with the example we started on in the first week.  The current leap year system was established in 1582 by Pope Gregory I (hence, the name "Gregorian calendar") so we only need to consider years greater than 1582.  Leap years are all the years divisible by 4.  However, years divisible by 100 are not leap years.   As a final correction, years divisible by 400 are leap years.  Thus, the rule is:

        Its a leap year if divisible by 4 and greater than 1582, unless the year is divisible by 100 and not by 400.

The circuit has the year as input (encoded as a BCD number of 4 digits or 16 bits) and the leap year flag as an output.  Assume that the year is greater than 1582 and that this bound does not need to be checked.

(a) Construct a circuit that determines if the year is divisible by 4.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

(b) Construct a circuit that determines if the year is divisible by 100.
 
 
 
 
 
 
 
 
 
 
 
 
 
 

(c) Construct a circuit that determines if the year is divisible by 400.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

(d) Finally, construct a circuit that outputs the leap year flag to be used by the month module we discussed in class.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

4. Sequential Logic (20 points)

You are debugging a circuit that has two flip-flops in a shift register configuration.  Users have detected anomalies in the behavior of the circuit and have asked you to find the problem.  The timing characteristics of the two flip-flops are as follows:

• the first has setup/hold/prop times of 2/3/4, respectively, and
• the second has times of 4/6/8.

(b) How would you correct it while leaving the flip-flops in place and adding only inverters with a propagation delay of 2?
 
 
 
 
 
 
 
 
 
 
 
 
 

(c) What is the smallest clock period that can be used on your corrected circuit that will still guarantee correct operation?  Explain.
 
 
 
 
 
 
 
 
 
 

5. Finite State Machine Design (25 points)

The circuit below consists of a shift-register (3 bits long) and a synchronous set-reset flip-flop.

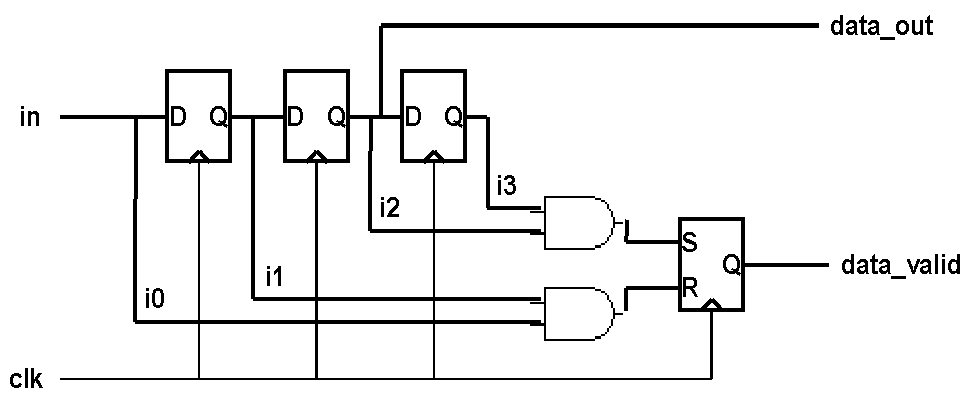
(a) Derive a state diagram for the state machine composed of the single set-reset flip-flop.  The inputs to this machine are S and R.  Assume that the two inputs will never both be 1 simultaneously.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

(b) Derive the state table for this state machine.
 
 
 
 
 
 
 
 
 
 
 
 

(c) Re-implement the FSM using a single D flip-flop instead of a S-R flip-flop.  Make sure to minimize your expression for D.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

(d) What does the entire circuit (1-bit FSM + 3-bit shift-register) do?